What is K-Nearest Neighbor Algorithm?

K-Nearest Neighbor (KNN) is a supervised machine learning algorithm used for classification and regression. In a KNN model, the output for a new data point is based on the “K” nearest data points in the training data set.

Demystifying the K-Nearest Neighbor (K-NN) Algorithm

In the realm of machine learning and data science, the K-Nearest Neighbor (K-NN) algorithm stands as a simple yet powerful technique for classification and regression tasks. Its intuitive concept, flexibility, and ease of implementation make it a fundamental tool in any data scientist’s toolkit. In this blog post, we will explore the principles behind the K-NN algorithm, its applications, strengths, weaknesses, and practical considerations.

Understanding the K-Nearest Neighbor Algorithm

At its core, the K-Nearest Neighbor algorithm is a non-parametric, instance-based machine learning algorithm used for both classification and regression tasks. The primary idea behind K-NN is to predict the class or value of a data point based on the majority class or average value of its K nearest neighbors in the feature space.

Key Components of K-NN:

1. Dataset:  K-NN relies on a labeled dataset, which means that each data point is associated with a known class label (for classification) or a target value (for regression).

2. Distance Metric:  To determine the proximity of data points, a distance metric is used, most commonly the Euclidean distance in a multidimensional feature space. Other distance metrics like Manhattan or Minkowski distance can also be employed depending on the problem.

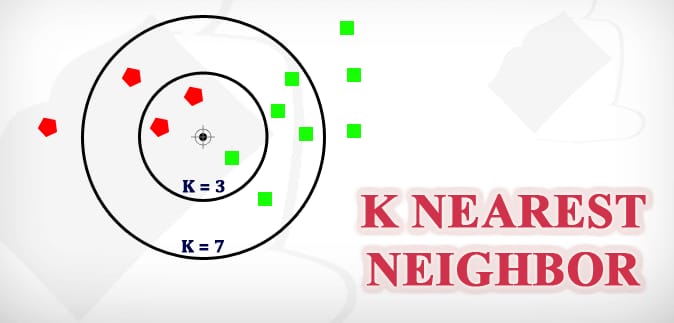
3. K-Value:  K represents the number of nearest neighbors that the algorithm considers when making a prediction. The choice of K is crucial and should be determined through experimentation.

How the K-NN Algorithm Works

1. Initialization:  Begin by selecting a value for K and a distance metric.

2. Prediction:  For a given data point (the one you want to classify or predict), calculate the distance between it and all other data points in the dataset using the chosen distance metric.

3. Nearest Neighbors:  Select the K data points with the smallest distances to the target data point. These are the “nearest neighbors.”

4. Majority Vote (Classification):  If you are using K-NN for classification, let the class labels of the K nearest neighbors “vote.” The class that appears the most among these neighbors becomes the predicted class for the target data point.

5. Average (Regression):  If K-NN is used for regression, calculate the average of the target values of the K nearest neighbors. This average becomes the predicted value for the target data point.

Applications of K-NN

K-NN is a versatile algorithm with various practical applications:

1. Image Classification:  In computer vision, K-NN can be used to classify images based on their features or pixel values.

2. Recommendation Systems:  K-NN powers collaborative filtering in recommendation systems by finding users with similar preferences and recommending items liked by their nearest neighbors.

3. Anomaly Detection:  K-NN can identify anomalies or outliers in datasets by flagging data points that have dissimilar neighbors.

4. Medical Diagnosis:  In healthcare, K-NN can help predict disease outcomes or diagnose conditions by analyzing patient data and finding similar cases from historical records.

5. Natural Language Processing:  In text classification tasks, such as sentiment analysis, K-NN can classify documents based on their word vectors.

Strengths of K-NN

1. Simple Concept:  K-NN’s simplicity makes it easy to understand and implement, making it an excellent choice for beginners in machine learning.

2. No Training Required:  K-NN is non-parametric, meaning it doesn’t require a training phase. The model directly uses the training data for predictions.

3. Flexibility:  K-NN can be used for both classification and regression tasks, making it adaptable to various types of problems.

4. Interpretability:  The algorithm’s predictions are interpretable, as they are based on the actual data points in the dataset.

5. Robustness:  K-NN can handle noisy data and doesn’t make strong assumptions about the underlying data distribution.

Weaknesses and Considerations

While K-NN has its merits, it also has some limitations and considerations:

1. Computational Complexity:  As the dataset grows, the computation of distances to all data points can become computationally expensive.

2. Choice of K:  The choice of the K value is crucial and can significantly impact the model’s performance. Selecting an inappropriate K can lead to underfitting or overfitting.

3. Sensitive to Noise:  K-NN is sensitive to noisy data and outliers, which can influence the results significantly.

4. Curse of Dimensionality:  K-NN’s performance can deteriorate as the dimensionality of the feature space increases. High-dimensional spaces make it difficult to find meaningful nearest neighbors.

5. Imbalanced Data:  In classification tasks with imbalanced class distributions, K-NN may favor the majority class, leading to biased predictions.

The K-Nearest Neighbor (K-NN) algorithm is a straightforward yet powerful tool in the realm of machine learning and data science. Its simplicity, flexibility, and interpretability make it a valuable addition to the data scientist’s toolkit. By understanding the fundamental principles of K-NN, choosing the appropriate K value, and handling its limitations, practitioners can harness its potential for a wide range of applications, from image classification and recommendation systems to anomaly detection and medical diagnosis.

In the ever-expanding landscape of machine learning algorithms, K-NN serves as a reminder that sometimes the simplest methods can yield impressive results, especially when used judiciously and in the right context. Whether you’re just starting your journey in machine learning or are a seasoned practitioner, K-NN remains a valuable and versatile technique worth exploring and mastering.